Dot product matrix

Each dot product operation in matrix multiplication must follow this rule. Dot products are done between the rows of the first matrix and the columns of the second matrix. Thus, the rows of the first matrix and columns of the second matrix must have the same length.

I want to emphasize an important point here. The biggest takeaway is: dot product of two 1-dimensional datain a scalar number. Matrix multiplication is not commutative. Two matrices can be multiplied using the dot () method of numpy.

C = dot (A,B ) returns the scalar dot product of A and B. If A and B are vectors, then they must have the same length. In this case, the dot function treats A and B as collections of vectors. We match the price to how many sol multiply each, then sum the result.

In other words: The sales for Monday were: Apple pies: $3×13=$3 Cherry pies: $4×8=$3 and Blueberry pies: $2×6=$12. We define the matrix-vector product only for the case when the number of columns in A equals the number of rows in x. Compute the matrix multiplication between the DataFrame and other. This method computes the matrix product between the DataFrame and the values of an other Series, DataFrame or a numpy array.

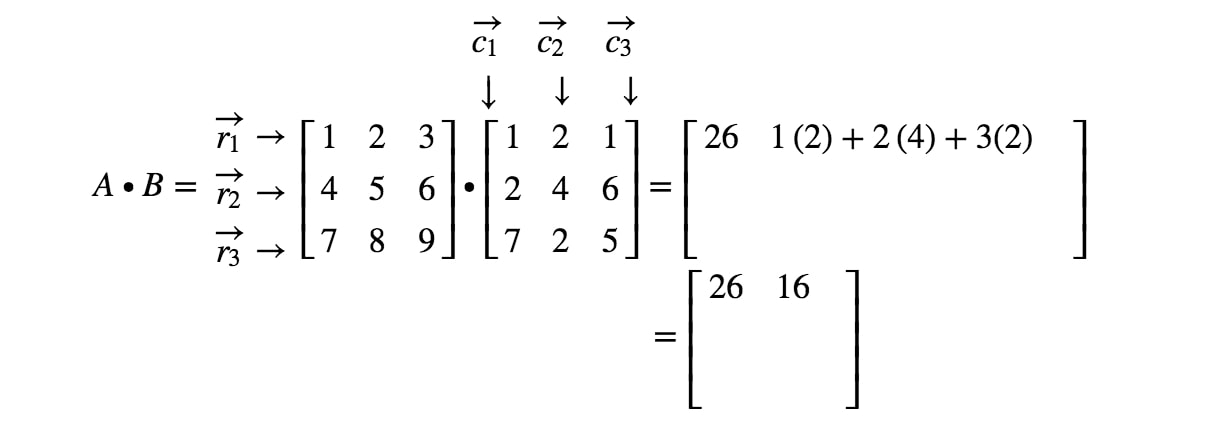
Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. The dot product of these two vectors is sum of products of elements at each position.

Since we multiply elements at the same positions, the two vectors must have same length in order to have a dot product. In the field of data science, we mostly deal with matrices. A matrix is a bunch of row and column vectors combined in a structured way. Thus, multiplication of two matrices involve many dot product operations of vectors.

Here, is the dot product of vectors. C(AT) is a subspace of N(AT) is a subspace of Observation: Both C(AT) and N(A) are subspaces of. Might there be a geometric relationship between the two?

Dot product of vectors and matrices (matrix multiplication) is one of the most important operations in deep learning. This is why the number of columns in the first matrix must match the number of rows of the second.

So: The columns of AT are the rows of A. The rows of AT are the columns of A. Let’s start out in two spatial dimensions. Below is the dot product of $2$ and $3$. Two vectors must be of same length, two matrices must be of the same size.

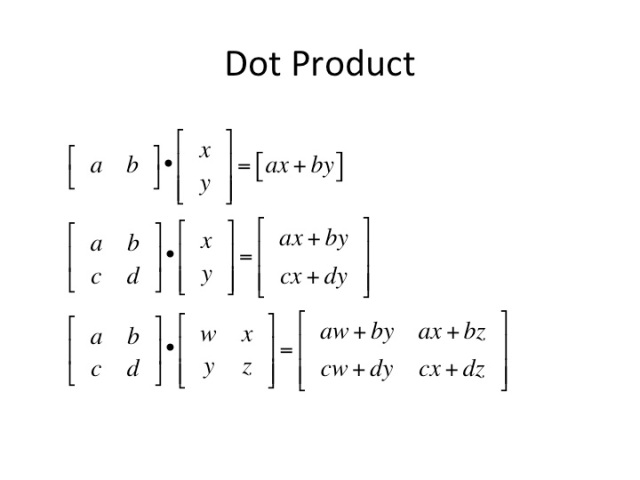
If x and y are column or row vectors, their dot product will be computed as if they were simple vectors. This function returns a scalar product of two input vectors, which must have the same length. It returns the matrix product of two matrices, which must be consistent, i. None) ¶ Dot product of two arrays.

Specifically, If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation). For instance, you can compute the dot product with np. In Euclidean geometry, the dot product between the Cartesian components of two vectors is often referred to as the inner product. Just by looking at the dimensions, it seems that this can be done.

Here is an example: It might look slightly odd to regard a scalar (a real number) as a "x 1" object, but doing that keeps things consistent. Representing the vectors $u$ and $v$ as 1D arrays, we write the script below to compute their dot product. NumPy has the numpy.

From the docs: The method computes a dot - product of two matrices. The vectors must have the same size and type. So in the dot product you multiply two vectors and you end up with a scalar value. If the matrices have more than one channel, the dot products from all the channels are summed together.

So the dot product of this vector and this vector is 19. This page aims to provide an overview and some details on how to perform arithmetic between matrices, vectors and scalars with Eigen.

Let me do one more example, although.